ITALIAN CHEMIST
1776–1856
AVOGADRO'S NUMBER A principle stated in 1811 by the Italian chemist Amadeo Avogadro (1776-1856) that equal volumes of gases at the same temperature and pressure contain the same number of molecules regardless of their chemical nature and physical properties.This number (Avogadro's number) is 6.023 X 10 23.It is the number of molecules of any gas present in a volume of 22.41 L and is the.
In 1811, just three years after John Dalton published his atomic theory , a brilliant theoretician named Amedeo Avogadro proposed his molecular theory. Avogadro's molecular theory related gas densities to molecular weights, explained reacting proportions by volume in terms of molecular ratios and compositions, and suggested methods for determining both molecular weights and compositions. His 1811 publication was a tour de force. Nonetheless, it was ignored for over half a century. Historians have sought reasons for the neglect of Avogadro's work in his life, his theory, and the state of chemistry at the time.
Avogadro's Life
Avogadro's Law is one of the most important laws to gas chemistry, but it wasn't always viewed this way. In this lesson we will learn how Amedeo Avogadro came up with this law and how it is used. In order to tackle molecular simulation and visualization challenges in key areas of materials science, chemistry and biology it is necessary to move beyond fixed software applications. The Avogadro project is in the final stages of an ambitious rewrite of its core data structures, algorithms and visualization capabilities. Avogadro is best known today for his eponymous gas law, which states that equal volumes of gasses, at the same temperature and pressure, contain the same number of molecules.
Amedeo Avagadro was born in 1776 in Turin, a city in northwestern Italy. Avogadro spent his entire life within 80 kilometers (50 miles) of Turin, far from the cultural centers where chemistry was becoming a science. He received a classical education in the humanities, earned a doctorate in law in 1796 at the age of twenty, and practiced law for the next ten years. After auditing some courses and studying science on his own, Avogadro made a radical career change. In 1806 he became a secondary school science teacher, and in 1820 a university physics professor. He married in 1815, had seven children, and by all accounts, led a very happy family life.

During his academic career, Avogadro's publications revealed an intense curiosity, sharp intuition, vivid imagination, rigorous logic, and independent judgment—traits of an outstanding scientist. His obituary in an Italian scientific journal remarked on his retiring disposition and on the simplicity of his life, and it noted his other researches, but it did not mention the 1811 paper on his molecular theory.
Avogadro's Molecular Theory
Avogadro made two assumptions about molecules in his 1811 publication. The first assumption is now known as Avogadro's hypothesis, sometimes also called the EVEN hypothesis. It stated that equal volumes of gases contain equal numbers (thus, even) of molecules at the same temperature and pressure. The hypothesis was based on a model of the gas state in which molecules are far apart and equally spaced so that each molecule occupies the same volume. The second assumption was that gas molecules can divide during chemical reactions.
Avogadro used the EVEN hypothesis to interpret gas densities and assign molecular weights. EVEN implies that the density of a gas at a given temperature and pressure depends only on the weight of its molecules. Avogadro supposed that since the reported gas density of oxygen was 15 times that of hydrogen, the molecular weight of oxygen was 15 times that of hydrogen (the modern calculation of the ratio of the densities and molecular weights is actually sixteen). Consequently, he assigned oxygen a molecular weight of 15, relative to 1 for hydrogen. By this method Avogadro could determine a molecular weight for any gas, given its density.
Avogadro needed both assumptions to explain reacting proportions and molecular compositions. For example, when water forms, the reacting proportions of hydrogen, oxygen, and water are 2:1:2 by volume. On the basis of the EVEN hypothesis, a 2:1:2 volumetric ratio should correspond to a 2:1:2 molecular ratio. Thus, two molecules of hydrogen (h) should combine with one molecule of oxygen (o) to give two molecules of water. Direct combination, however, would give only one molecule of h 2 o. To fit the volumetric data, Avogadro split the h 2 o water molecule into two ho 1/2 molecules. This in turn forced him to assume that oxygen molecules could divide into two 'half molecules' during the reaction: 2h + o → [h 2 o] → 2ho 1/2 . He expressed the composition of water as one 'half molecule' of oxygen combined with one molecule of hydrogen (ho 1/2 ). With the aid of his two assumptions—EVEN and divisible molecules—Avogadro determined compositions for water, ammonia, hydrogen chloride, and gaseous oxides of nitrogen, carbon, and sulfur.
Early Nineteenth-Century Chemistry
The state of chemical theory and practice in 1811 was primitive by modern standards and not yet ready for Avogadro's molecular theory. Dalton's model of the gas state (atoms of different size in contact) precluded EVEN. Jöns Jakob Berzelius, another very influential chemist, believed gaseous elements like oxygen contained only indivisible atoms, not divisible molecules. Gas density and combining ratios data were limited and inaccurate. Atomic weights depended on unknown formulas and vice versa—a vicious cycle.
Conclusion
In retrospect the neglect of Avogadro's theory seems quite understandable. In 1811 he was a secondary school teacher living in a remote province. Furthermore, he was a theoretical physicist writing for practical chemists in legal language. His molecular theory was based on speculative assumptions, lacked independent experimental evidence or theoretical justification, and could only explain but not predict volumetric ratios. His molecular ratios (2h + o → 2ho 1/2 ) were far removed from modern atomic ratios (2H 2 + O 2 → 2H 2 O) and did not solve the atomic weight –formula problem. Chemists in the early nineteenth century, however, needed more immediately productive theories and much more experimental information before Avogadro's theory could be truly useful. It took half a century of effort, the development of organic chemistry, and the ingenuity of another Italian, Stanislao Cannizzaro, to build a modern chemistry on the foundations laid by Avogadro. Nonetheless, as Nobel Prize winner Linus Pauling observed in a 1956 article in Science , Avogadro's work 'forms the basis of the whole of theoretical chemistry' and is 'one of the greatest contributions to chemistry that has ever been made.'
SEE ALSO Berzelius, JÖns Jakob ; Cannizzaro, Stanislao ; Dalton, John ; Pauling, Linus .
John D. Hostettler
Bibliography
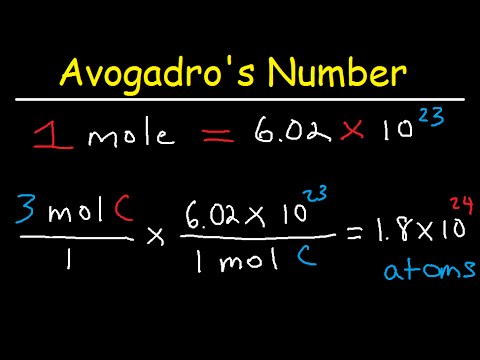
Causey, Robert L. (1971). 'Avogadro's Hypothesis and the Duhemian Pitfall.' Journal of Chemical Education 48(6):365–367.
Ihde, Aaron (1964). The Development of Modern Chemistry. New York: Harper & Row.
Lipeles, Enid S. (1983). 'The Chemical Contributions of Amedeo Avogadro.' Journal of Chemical Education 60(2):127–128.
Nash, Leonard K. (1957). 'The Atomic-Molecular Theory.' In Harvard Case Histories in Experimental Science , Vol. 1, ed. James Bryant Conant. Cambridge, MA: Harvard University Press.
Pauling, Linus (1956). 'Amedeo Avogadro.' Science 124:708–713.

Learning Objective
- Define and memorize Avogadro’s number
Key Points
- The mole allows scientists to calculate the number of elementary entities (usually atoms or molecules) in a certain mass of a given substance.
- Avogadro’s number is an absolute number: there are 6.022×1023 elementary entities in 1 mole. This can also be written as 6.022×1023 mol-1.
- The mass of one mole of a substance is equal to that substance’s molecular weight. For example, the mean molecular weight of water is 18.015 atomic mass units (amu), so one mole of water weight 18.015 grams.
Term
- moleThe amount of substance of a system that contains as many elementary entities as there are atoms in 12 g of carbon-12.
The chemical changes observed in any reaction involve the rearrangement of billions of atoms. It is impractical to try to count or visualize all these atoms, but scientists need some way to refer to the entire quantity. They also need a way to compare these numbers and relate them to the weights of the substances, which they can measure and observe. The solution is the concept of the mole, which is very important in quantitative chemistry.
Avogadro’s Number
Amadeo Avogadro first proposed that the volume of a gas at a given pressure and temperature is proportional to the number of atoms or molecules, regardless of the type of gas. Although he did not determine the exact proportion, he is credited for the idea.
Avogadro’s number is a proportion that relates molar mass on an atomic scale to physical mass on a human scale. Avogadro’s number is defined as the number of elementary particles (molecules, atoms, compounds, etc.) per mole of a substance. It is equal to 6.022×1023 mol-1 and is expressed as the symbol NA.
Avogadro’s number is a similar concept to that of a dozen or a gross. A dozen molecules is 12 molecules. A gross of molecules is 144 molecules. Avogadro’s number is 6.022×1023 molecules. With Avogadro’s number, scientists can discuss and compare very large numbers, which is useful because substances in everyday quantities contain very large numbers of atoms and molecules.
The Mole
The mole (abbreviated mol) is the SI measure of quantity of a “chemical entity,” such as atoms, electrons, or protons. It is defined as the amount of a substance that contains as many particles as there are atoms in 12 grams of pure carbon-12. So, 1 mol contains 6.022×1023 elementary entities of the substance.
Chemical Computations with Avogadro’s Number and the Mole
Avogadro’s number is fundamental to understanding both the makeup of molecules and their interactions and combinations. For example, since one atom of oxygen will combine with two atoms of hydrogen to create one molecule of water (H2O), one mole of oxygen (6.022×1023 of O atoms) will combine with two moles of hydrogen (2 × 6.022×1023 of H atoms) to make one mole of H2O.
Another property of Avogadro’s number is that the mass of one mole of a substance is equal to that substance’s molecular weight. For example, the mean molecular weight of water is 18.015 atomic mass units (amu), so one mole of water weight 18.015 grams. This property simplifies many chemical computations.
If you have 1.25 grams of a molecule with molecular weight of 134.1 g/mol, how many moles of that molecule do you have?
[latex]1.25g times frac{ 1 text{ mole}}{134.1g}=0.0093 text{ moles}.[/latex]
Show SourcesBoundless vets and curates high-quality, openly licensed content from around the Internet. This particular resource used the following sources:
http://www.boundless.com/
Boundless Learning
CC BY-SA 3.0.
http://www.chem1.com/acad/webtext/intro/int-2.html#SEC2
Steve Lower’s Website
CC BY-SA.
http://en.wiktionary.org/wiki/mole
Wiktionary
CC BY-SA 3.0.
Avogadro Chemistry Software
http://en.wikipedia.org/wiki/Mole_(unit)
Wikipedia
CC BY-SA 3.0.
http://en.wikipedia.org/wiki/Avogadro_constant
Wikipedia
CC BY-SA 3.0.
Avogadro Chemistry Competition
http://en.wikipedia.org/wiki/Avogadro_constant%23mediaviewer/File:Avogadro_Amedeo.jpg
Wikimedia
Public domain.
